1457. “Sort” station
At the “Sorting” railway
station on the way there are n railroad
cars, out of which it is necessary to form the railway train. All cars have the
same length, but different cargoes are arranged at them, so the cars may have
different weights. The workers of the “Sort” train station should order the
cars in ascending weight, then the train is allowed to go.
Usually for such purposes
the so-called shunting locomotives and electric locomotives are used, but at
this station the experimental device for sorting cars is used. It is assumed
that it will significantly reduce the time required for forming trains.
This device is moved on an
air cushion above the cars, its length is slightly greater than the length of
the two cars. It can hang on two adjacent cars, pick them both in the air and
interchange. However, the device lifting capacity is limited: the operation can
be carried out if the total mass of the two cars does not exceed M.
Your task is to write a
program that determines whether it is possible to sort the cars on the rails
with the help of experimental device in the demanding order.
Input. The first line contains the
number of cars n (2
≤ n ≤ 105) and the lift capacity of
experimental device M (2
≤ M ≤ 109). The second line contains the
weights of the cars m1, m2, ..., mn (for these weights the equalities 1 ≤ mi ≤ 109 hold, the car weights are
pairwise distinct). The weights of the cars are listed in the order in which
they are located initially on the railway.
Output. Print “Yes”, if its possible
to sort the cars with the help of experimental device, and “No” otherwise.
|
Sample input |
Sample output |
|
4 10 5 6 3
4 |
Yes |
SOLUTION
sort
Algorithm analysis
To sort the cars, we will use
exchange sorting. However, the task requires not to sort the cars, but to determine whether it is
possible. For this, for each adjacent pair of cars for which mi > mi+1,
swap the cars with numbers i and i + 1. If there is an i such
that mi > mi+1 and mi + mi+1 > M, then sorting cannot be performed.
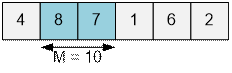
Calculate in the variable mx the maximum among the numbers m1, m2,
…, mi. If the next value mi+1 is less than mx, then the car of mass mx must be swapped with the car of mass mi+1 during the
exchange sorting process. If for some i
the inequality mx + mi+1 > M holds and, in addition, mx > mi+1, then sorting is impossible. Otherwise,
the cars can be sorted in increasing order of their masses.
Example
Let M = 10. Consider the next sample.
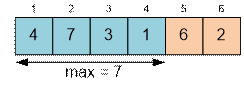
Consider the fifth element: m[5] = 6. The maximum element mx before it is 7 (m[2] = 7). The car
with mass of 6 must stand before the car with mass of 7, therefore these cars
should be interchanged. However, this is impossible, since their masses are
greater than M: m[2] + m[5] > M or 7 + 6 > 10.
If, for example,
a car with mass of 8 is in the fifth position, then the desired rearrangement is possible,
since the cars
with masses of 7 and 8 do not need to be swapped.
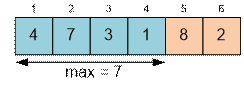
Exercise
Simulate the solution for the next
samples.

Algorithm realization
Read the input
data. Process sequentially the masses of cars.
scanf("%d %d",&n,&M);
while(n--)
{
scanf("%d",&val);
Sorting cars is impossible if the break statement is
executed at least once. In this case, n will be
non-negative.
if ((val <
mx) && (val + mx > M)) break;
if (val >
mx) mx = val;
}
If all car
masses are processed in the while loop, then n = -1, and sorting of cars is possible.
Otherwise, it is impossible to arrange the cars in the required way.
if (n >= 0) printf("No\n"); else
printf("Yes\n");
Java realization
import java.util.*;
class Main
{
public static void
main(String[] args)
{
Scanner con = new Scanner(System.in);
int n =
con.nextInt();
int M =
con.nextInt();
int max = 0;
while(n-- > 0)
{
int val = con.nextInt();
if (val <
max && val + max > M) break;
if (val >
max) max = val;
}
if (n >= 0)
System.out.println("No\n");
else
System.out.println("Yes\n");
con.close();
}
}